КПД
Программный комплекс, реализующий компьютерную психологическую диагностику и статистическую обработку психологических исследований.
Включает 919 методик. Программа кроссплатформенна — низкие системные требования и широкий спектр поддержки операционных систем Microsoft — от DOS и Windows 95 до Windows 11.
Мы не понаслышке знаем о тех затруднениях, которые испытывают как студенты, так и преподаватели с доказательной частью своей научной работы, требующей огромных затрат времени и монотонного труда при обсчёте результатов проведённых психодиагностических исследований в больших выборках испытуемых. Выполнение подобной работы вручную — длительный и трудоёмкий процесс, большинство же существующих статистических программ обладают широкими возможностями и универсальны по своему назначению, однако они сложны для психологов и тем более для студентов психологических факультетов, работающих над своими курсовыми и дипломными проектами и требуют достаточно обширных знаний в области математической статистики.
Разработанная нами программа ориентирована на профессиональных психологов и очень проста в применении. После загрузки первичных результатов исследования можно сразу же получить статистическую информацию, достаточную для написания любой научной работы: от курсовой до диссертации. Основанием для разработки данной программы математико-статистической обработки данных послужил собственный опыт научно-исследовательской работы, все те трудности при обработке данных, которые пришлось испытать самим и нашим студентам.
Программа позволяет качественно оформлять текстовую документацию в связи с встроенным графическим редактором и возможностью выхода в Microsoft Word и Excel, благодаря чему можно буквально нажатием одной клавиши вставить полученные таблицы и диаграммы в текст своей научной работы.
ДИАГНОСТИКА
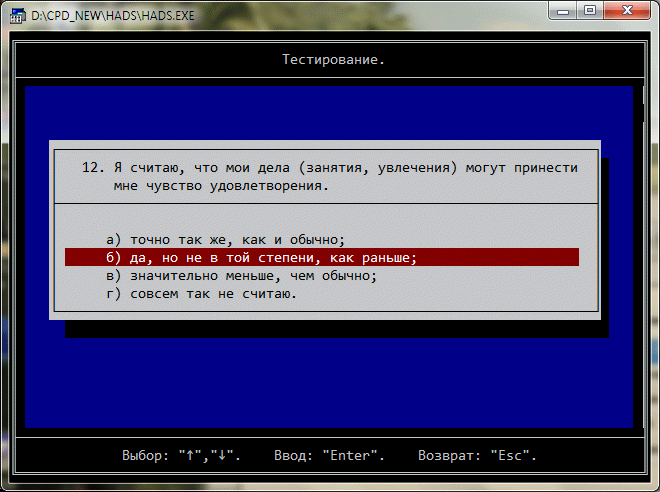
Термин "компьютерная психологическая диагностика" требует уточнения. Вместо термина "Компьютерная психологическая диагностика" следовало бы использовать термин "Психологическая диагностика и консультирование с применением компьютерных технологий". Психологической диагностикой занимается не компьютер, а психолог. Применение компьютерных технологий в данной сфере деятельности это не более, чем создание эффективных виртуальных продолжений профессиональных знаний, опыта и способностей дипломированного психолога. И именно психолог несёт всю нравственную и юридическую ответственность за корректное применение результатов тестирования. В нашем исследовании было установлено, что сам факт применения компьютерных версий психодиагностических методик даёт достаточно значительные отличия от стандартного "бумажного" оригинала. Наиболее существенное влияние на точность результатов тестирования оказывают различные социально-психологические феномены, возникающие при проведении тестирования.
Сама ситуация тестирования. В ситуации "клиента" и в ситуации "экспертизы" тестовые показатели некоторых тестовых шкал у одного и того же испытуемого могут быть различными, а в ряде случаев даже сильно искаженными. Непротиворечивые заключения — это, прежде всего, искусство и профессионализм психолога, а не результат применения формальной логики, которая и составляет основу всех цифровых технологий. Использование в непосредственной работе с обследуемым компьютерных технологий выходит за рамки обычной психодиагностики и далеко ею не исчерпывается.
Так что же может современный компьютер применительно к профессиональной деятельности психолога?
1. Объём и хранение базы знаний и базы данных. Объёмы информации, которые могут хранить современные носители компьютерной памяти, значительно превышают возможности памяти одного психолога. И оперативной и долговременной.
2. Разнообразие типов хранимой информации. Тексты, графические изображения, аудиозаписи, видеофильмы, программы тестирования, математической и статистической обработки результатов исследования, аудио и визуального сопровождения всех процессов психологической диагностики и консультирования. И это намного больше, чем просто "бумажная" психодиагностика.
3. Точность хранения информации. Не вызывает сомнения. Байт в байт. Контрольная копия гарантирует длительность хранения и возможность быстрого воспроизведения.
4. Компактность носителя информации. Один пример: USB Flash RAM. Размер: меньше коробки спичек. Объём информации: персональная научная библиотека по специальности. Всегда с собой. Компьютер практически в каждом учреждении и в каждом доме.
5. Скорость обработки и поиска информации. Технический прогресс в области создания компьютерного "железа", а также в сфере разработки программного обеспечения идёт такими темпами, что производительность цифровых методов обработки информации превышает возможности не только одного психолога, но целого коллектива специалистов.
6. Мобильность. Если "флешка" с персональной базой знаний всегда с собой, то приступить к работе на новом рабочем месте и в другом городе можно практически сразу же после включения компьютера.
7. Новые технологии психологической диагностики. Пример: технология преодоления "психологической защиты". Компьютерное тестирование — это процедура обследования, а не заполнение "бумажного" бланка тестирования. "Шкала достоверности" или «шкала лжи» в компьютерном варианте — это предупреждающая, "обучающая" и диагностическая процедура. Если критическое значение по этой шкале в процессе тестирования превышает допустимое, компьютерная программа может вернуть обследуемого к первому пункту вопросника и предупредить о необходимости быть более искренним. Количество подобных повторов имеет не только диагностическое значение, но и меняет весь ход психологической диагностики.
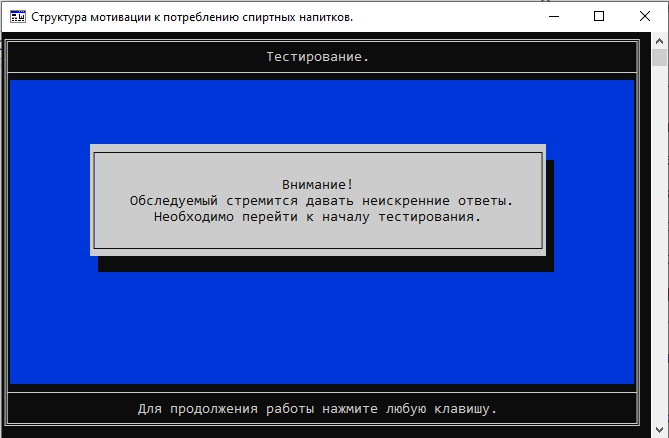
А ещё компьютерная программа в автоматическом режиме может фиксировать время ответа (вплоть до миллисекунд) на каждый пункт тестового опросника. Данная информация имеет дополнительное диагностическое значение и не может быть получена в ходе обычного тестирования.
8. Новые технологии психологического консультирования. Психологическая диагностика и психологическое консультирование это две взаимосвязанные стороны одного процесса. Применение компьютерных технологий оказывает психологическое воздействие на эмоциональные состояния, мнения, убеждения и мировоззрение клиента. Предъявление графических изображений результатов тестирования в форме различных графиков и диаграмм, а также текстов интерпретаций, имеющих разное эмоционально-оценочное значение, в зависимости от задачи консультирования имеет особое значение, выходящее за рамки только психодиагностики. Примеры практического применения. Графическая форма результатов тестирования с помощью компьютерной версии методики "Диагностика алкогольной болезни" позволяет в той или иной степени преодолевать алкогольную анозогнозию и наглядно продемонстрировать клиенту его истинный уровень алкогольных проблем в сравнении с "обычным" клиентом наркологического стационара. С диагностической точки зрения по отношению к клиенту с установленным диагнозом "алкогольная зависимость" применение этой методики не имеет никакого смысла. С точки зрения психологического воздействия имеет. И работает.

Другой пример. Графическая форма результатов тестирования с помощью компьютерной версии методики «Таблицы Шульте» оказывает достаточно выраженное воздействие на обследуемого в плане формирования качественной мотивации к прохождению курса лечения – проверено многократно. Нарушения умственной работоспособности и функций активного внимания могут диагностироваться при многих заболеваниях и состояниях, включая неврозы, атеросклероз, зависимость от алкоголя и разного рода психоактивных веществ. Обследуемый, наглядно видя на полученном графике свои результаты, старается их во что бы то ни стало улучшить, особенно когда это касается получения допуска к вождению автотранспортом, и стремится попасть на компьютерную диагностику повторно уже после прохождения курса терапии, что ставит данный процесс психодиагностики практически на один уровень с такими медицинскими диагностическими обследованиями как УЗИ или снятие электроэнцефалограммы.

Тексты интерпретаций, предназначенные для клиента — это не констатация факта наличия тех или иных эмоциональных состояний, особенностей характера, типа темперамента, отношений с окружающими или патопсихологических отклонений. Это ещё и прекрасный работающий метод психологического воздействия. И каждый такой текст должен быть индивидуальным, хорошо продуманным и основанным на всей имеющейся дополнительной информации о клиенте.
9. Новые невербальные методы воздействия. Хорошо известный факт. Защитная позиция клиента с закидыванием ноги на ногу и со скрещиванием рук на груди на 38% уменьшает восприятие информации и вызывает более критическое отношение к консультанту. Простое предложение психолога пройти психологические тестирование на компьютере снимает эту проблему. Чтобы отвечать на вопросы вербальной тестовой методики необходимо изменить позу и раскрыть руки. И это тоже не психодиагностика. Это метод психологического консультирования. Результат тестирования не всегда имеет значения. Установление контакта с клиентом — имеет значение всегда.
10. Удаленный вариант общения с клиентами и коллегами. Представление данных психологического обследования должно иметь респектабельный вид. Заключение психолога может быть "украшением" истории болезни в медицинском учреждении, а может быть "китайской грамотой", написанной неразборчивым почерком с использованием терминов малопонятных самому психологу. Оформление документации, которая передается клиентам на руки, имеет ещё большее значение. Профессионально составленное и красочно оформленное с помощью различных шрифтов, таблиц, диаграмм заключение с обязательными рекомендациями по решению психологических проблем клиента обладает эффектом последействия общения с консультантом. После выхода из кабинета психолога консультирование не заканчивается. Как показывает практика, все документы в течение определённого времени хранятся, изучаются и обсуждаются со знакомыми или родственниками клиента. "Виртуальное" присутствие личности психолога в повседневной жизни клиента — также является пролонгированным методом психологического воздействия.
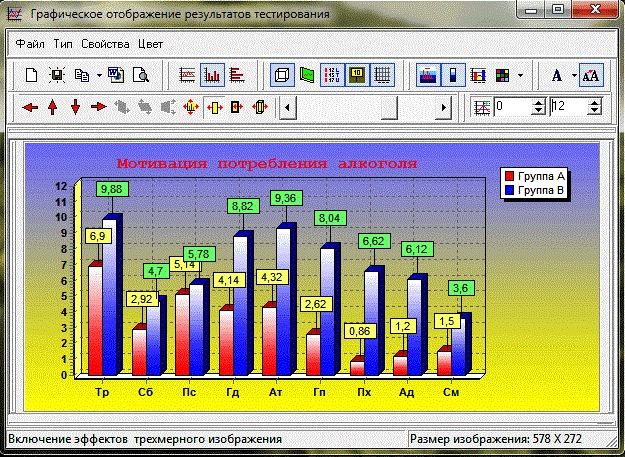
СТАТИСТИКА
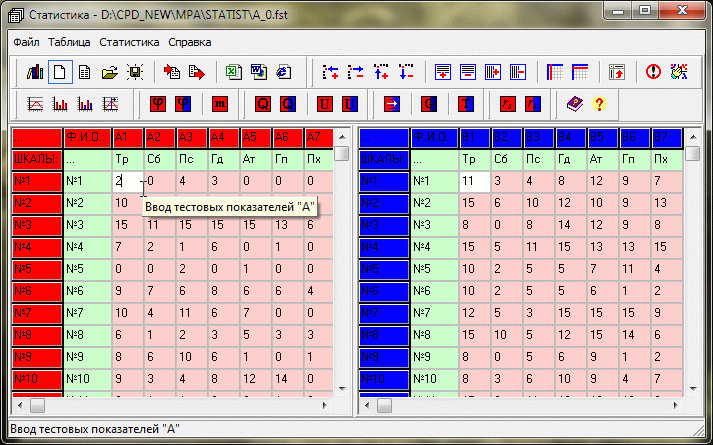
Необходимость в разработке специализированной для психологов программы статистической обработки возникла из личного практического опыта и анализа тех затруднений, которые испытывают студенты и преподаватели психологических факультетов с доказательной частью своей научной работы. Выполнение подобной задачи вручную — длительный и трудоемкий процесс, а большинство существующих компьютерных статистических программ требуют длительного изучения и достаточно сложны в применении.
Основная идея проекта — создание программы, которая бы позволяла психологу нажатием одной или нескольких клавиш компьютера сразу же получить всю необходимую статистическую информацию, достаточную для написания научной работы: от курсовой до диссертации. При этом следует иметь в виду, что невозможно создать такую программу, которая бы полностью освободила специалиста в области психологических исследований от элементарного незнания основ математической статистики.
Следующая цель разработки — качественное оформление текстовой документации полученных результатов психологических исследований. В этом смысле, нет никакой необходимости изобретать собственный "велосипед", так как существует неограниченно большое множество уже разработанных компьютерных программ, которые на высоком уровне справляются с этой задачей. Следовательно, текстовый отчёт по результатам компьютерной обработки данных должен иметь такой формат, который может быть легко "импортирован" во "внутренний" формат любой "внешней" программы. В качестве таких форматов были выбраны обычный не форматированный текст (.txt), формат веб-страницы (.html) и расширенный текстовый формат (.rtf). Единственное исключение — графический редактор построения диаграмм. В зависимости от типа личности визуальное представление результатов индивидуальной психологической диагностики (не с целью диагностики, а с целью психологического воздействия) должно иметь разный психологический смысл. Черно-белый схематический рисунок профиля личности графически точно отражающей все диапазоны возможных значений той или иной диагностической шкалы и персональную точку данного человека по тестируемому психологическому измерению, психологически "доступен" и "понятен" интроверту. Но подобная диаграмма или график "не понятен", и даже "обиден" для, т. н. "демонстративной" личности, которая требует красочного оформления своей "уникальности" и "неповторимости".
И еще одна проблема — в психологических исследованиях на малых выборках редко встречается т. н. "нормальное" статистическое распределение на которое любят ссылаться академические психологи. Поэтому, в данный программный пакет включены только непараметрические критерии оценки статистики, которые отражают специфические особенности психологических исследований и не вызывают вопросов у коллег. Из множества этих методов были выбраны наиболее известные и часто используемые психологами в научных публикациях. При необходимости применения более сложных методов статистики, накопленные эмпирические данные можно передать во внешнюю программу статистической обработки данных.
Для своей работы программа статистики может использовать не только файлы данных внутреннего формата, но и внешние текстовые файлы, а также позволяет вводить данные полученные "ручным" способом прямым вводом с клавиатуры компьютера. Все накопленные, импортированные или введённые выборки результатов тестирования можно конвертировать в обычный текстовый формат для их последующей передачи в другие внешние программы статистической обработки. Передача в Microsoft Excel осуществляется непосредственно из самой программы. Результаты проведённых статистических исследований в форме текстовых файлов можно сохранять в памяти компьютера, выводить на принтер или передавать в текстовый редактор Microsoft Word, не выходя из программы.
МЕТОДЫ И КРИТЕРИИ
СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ ПСИХОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ,
ВКЛЮЧЕННЫЕ В ДАННУЮ ПРОГРАММУ:
Оценка параметров распределения.
Параметры распределения - это его числовые характеристики, указывающие, где "в среднем" располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака.
1. Среднее арифметическое (оценка математического ожидания).
Средней величиной в статистике называется обобщающая количественная характеристика признака в статистической совокупности, отражающая типичный уровень этого признака в расчете на единицу совокупности. Наиболее распространенным видом средних является средняя арифметическая. Под средней арифметической понимается такое среднее значение признака, при замене которым индивидуальных значений признака суммарный объем этого признака по совокупности в целом сохраняется неизменным, т.е среднее арифметическое есть среднее слагаемое
На основе ошибки математического ожидания строятся доверительные интервалы. Если тестовый балл какого-либо испытуемого попадает в границы доверительного интервала, то нельзя считать, что испытуемый обладает повышенным (или пониженным) значением измеряемого свойства с заданным уровнем статистической значимости. Научные выводы требуют доказательств.
Усредненный графический профиль тестовых показателей по любой из предлагаемых методик можно получить нажатием одной клавиши.
2. Среднее квадратическое отклонение.
Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако два распределения, имеющие одинаковую среднюю арифметическую, могут значительно отличаться друг от друга по степени рассеяния (вариации) признака.
В качестве мер изменчивости результатов, характеризующих степень рассеивания отдельных величин вокруг средней арифметической, используются разные меры в зависимости от примененных шкал измерения. Для характеристики рассеивания величин интервальных шкал и шкал отношений чаще всего пользуются значением среднеквадратичного отклонения.
Среднее квадратическое отклонение — это среднее квадратическое из отклонений отдельных вариантов от их средней арифметической, т.е. показатель среднего отклонения от средней.
3. Дисперсия.
Дисперсия — это квадрат среднего квадратического отклонения. Она представляет собой средний квадрат отклонений вариантов от средней величины.
4. Коэффициент вариации.
Отношение квадратического отклонения к средней, выраженное в процентах, называется коэффициентом вариации. Коэффициент вариации используют также как характеристику совокупности данных исследования. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.
5. Коэффициент асимметрии (Аs) — показатель симметричности распределения.
Симметричным является распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных одновершинных распределений средняя арифметическая, мода и медиана равны между собой.
При левосторонней, или положительной, асимметрии в распределении чаще встречаются более низкие значения признака, а при правосторонней, или отрицательной — более высокие.
Величина Аs может изменяться от -1 до +1 (для одновершинных распределений). Чем ближе Аs по модулю к 1, тем асимметрия существеннее. Для симметричных распределений Аs= 0.
6. Эксцесс (Ex) — показатель островершинности распределения.
Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Он рассчитывается для симметричных распределений. В тех случаях, когда какие-либо причины способствуют преимущественному появлению средних или близких к средним значений, образуется распределение с положительным эксцессом. Если же в распределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двухвершинное.
Пример 1:
Оценка параметров распределения.
Пример 2:
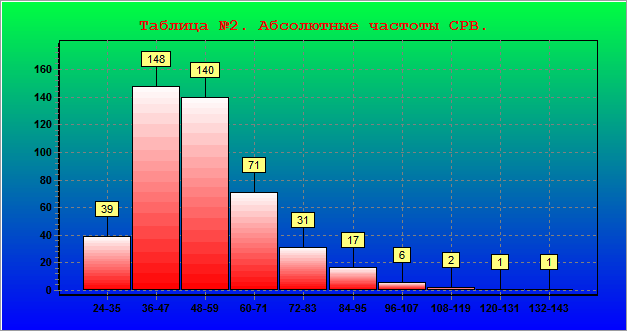
Частотная характеристика распределения тестовых показателей (абсолютные частоты)
Пример 3:
Частотная характеристика распределения тестовых показателей (накопленные частоты).
Пример 4:
Графическое отображение распределения тестовых показателей по одной из таблиц м. Шульте.
Классификация задач и методов их решения.
1. Выявление различий в уровне исследуемого признака.
Назначение методов: выявление различий между двумя выборками по уровню какого-либо признака, количественно измеренного.
Q — критерий Розенбаума.
Критерий применяется в тех случаях, когда данные представлены по крайней мере в порядковой шкале. Признак должен варьировать в каком-то диапазоне значений, иначе сопоставления с помощью Q-критерия просто невозможны. Например, если у нас только 3 значения признака, 1, 2 и 3, — нам очень трудно будет установить различия. Метод Розенбаума требует, следовательно, достаточно тонко измеренных признаков.
Диапазоны разброса значений в двух выборках должны не совпадать между собой, в противном случае применение критерия бессмысленно. Между тем, возможны случаи, когда диапазоны разброса значений совпадают, но, вследствие разносторонней асимметрии двух распределений, различия в средних величинах признаков существенны.
Пример 5:
Значимость различий по всем шкалам м. МПА по Q — критерию Розенбаума.
Пример 6:
Значимость различий по одноименным шкалам м. МПА по Q - критерию Розенбаума.
U - критерий Манна-Уитни.
Критерий позволяет выявлять различия между малыми выборками, когда n1,n2≥ 3 или n1=2, n2≥ 5, и является более мощным, чем критерий Розенбаума.
Ограничения критерия U:
1.В каждой выборке должно быть не менее 3 наблюдений; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.
2. В каждой выборке должно быть не более 60 наблюдений.
Пример 7:
Значимость различий по всем шкалам м. МПА по U - критерию Манна-Уитни.
Пример 8:
Значимость различий по одноименным шкалам м. МПА по U - критерию Манна-Уитни
Примечание: сравнение примеров по Q — критерию Розенбаума и U — критерию Манна-Уитни, которые были получены в одном и том же исследовании на одних и тех же выборках испытуемых, подтверждает, что U — критерий Манна-Уитни является более мощным и предпочтительным для практического применения.
Пример 9:
Графическое отображение различий в уровне исследуемого признака по шкалам м. МПА.
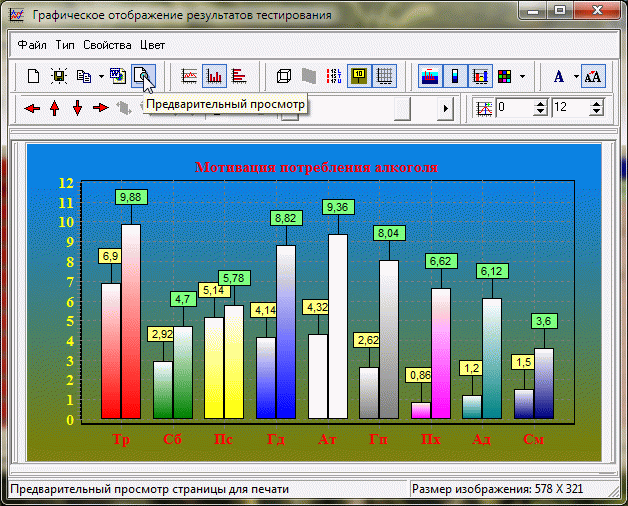
2. Оценка сдвига значений исследуемого признака.
G — критерий знаков.
Назначение критерия G: критерий знаков G предназначен для установления общего направления сдвига исследуемого признака. Он позволяет установить, в какую сторону в выборке в целом изменяются значения признака при переходе от первого измерения ко второму: изменяются ли показатели в сторону улучшения, повышения или усиления или, наоборот, в сторону ухудшения, понижения или ослабления. Критерий знаков применим как к тем сдвигам, которые можно определить лишь качественно, так и к тем сдвигам, которые могут быть измерены количественно.
Пример 10:
Оценка сдвига значений исследуемого признака по G — критерию знаков
Т — критерий Вилкоксона.
Назначение критерия: критерий применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность. С его помощью мы определяем, является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом.
Пример 11:
Оценка сдвига значений исследуемого признака по Т — критерию Вилкоксона.
3. Многофункциональные статистические критерии.
Многофункциональные статистические критерии — это критерии, которые могут использоваться по отношению к самым разнообразным данным, выборкам и задачам. Это означает, что данные могут быть представлены в любой шкале, начиная от номинативной (шкалы наименований). Это означает также, что выборки могут быть как независимыми, так и "связанными", то есть мы можем с помощью многофункциональных критериев сравнивать и разные выборки испытуемых, и показатели одной и той же выборки, измеренные в разных условиях.
Многофункциональные критерии позволяют решать задачи сопоставления уровней исследуемого признака, сдвигов в значениях исследуемого признака и сравнения распределений.
Многофункциональные критерии построены на сопоставлении долей, выраженных в долях единицы или в процентах. Суть критериев состоит в определении того, какая доля наблюдений (реакций, выборов, испытуемых) в данной выборке характеризуется интересующим исследователя эффектом и какая доля этим эффектом не характеризуется.
Таким эффектом может быть:
а) определенное значение качественно определяемого признака;
б) определенный уровень количественно измеряемого признака;
в) определенное соотношение значений или уровней исследуемого признака.
Путем сведения любых данных к альтернативной шкале "Есть эффект — нет эффекта" многофункциональные критерии позволяют решать все три задачи сопоставлений — сравнения "уровней", оценки "сдвигов" и сравнения распределений.
Критерий φ* применяется в тех случаях, когда обследованы две выборки испытуемых, биномиальный критерий m — в тех случаях, когда обследована лишь одна выборка испытуемых.
Одним из преимуществ многофункциональных критериев является возможность формулировки достаточно большого количества статистических гипотез, что позволяет извлечь максимум полезной информации из одного проведенного исследования.
Пример 12:
Выбор варианта статистической гипотезы по биномиальному критерию m
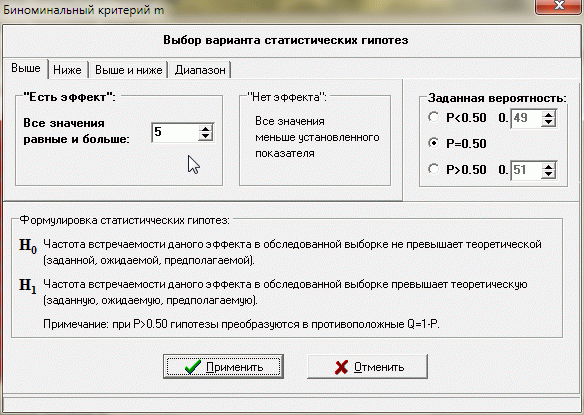
Критерий φ * — угловое преобразование Фишера.
Назначение критерия φ *: критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта.
Данный критерий позволяет:
1) сопоставлять выборки по качественно определенному критерию;
2) сопоставлять выборки по количественно определенному критерию;
3) сопоставлять выборки и по уровню и по распределению признака.
Пример 13:
Статистическая значимость различий по всем шкалам м. МПА по критерию φ *
Биномиальный критерий m.
Назначение критерия m: критерий предназначен для сопоставления частоты встречаемости какого-либо эффекта с теоретической или заданной частотой его встречаемости. Он применяется в тех случаях, когда обследована лишь одна выборка объемом не более 300 наблюдений, в некоторых задачах — не больше 50 наблюдений.
Биномиальный критерий m позволяет оценить, насколько эмпирическая частота интересующего нас эффекта превышает теоретическую, среднестатистическую или какую-то заданную частоту, соответствующую вероятности случайного угадывания, среднему проценту успешности в выполнении данного задания, допустимому проценту брака и т.п.
Биномиальный критерий незаменим, если налицо 2 условия:
а) обследована лишь одна выборка испытуемых, и нет возможности или смысла делить эту выборку на две части с целью дальнейшего применения критерия φ *, так как для нас по каким-то причинам важно исследовать частоту встречаемости признака в выборке в целом;
б) в обследованной выборке менее 30 испытуемых, что не позволяет нам применить критерий χ2.
Пример 14:
Проверка статистической гипотезы по биномиальному критерию m
4. Коэффициент корреляции.
Коэффициент ранговой корреляции Спирмена.
Назначение: метод ранговой корреляции позволяет определить тесноту (силу) и направление корреляционной связи между двумя признаками или двумя профилями (иерархиями) признаков.
Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы. Такими рядами значений могут быть:
1. Два признака, измеренные в одной и той же группе испытуемых.
В данном случае ранжируются индивидуальные значения по первому признаку, полученные разными испытуемыми, а затем индивидуальные значения по второму признаку. Если два признака связаны положительно, то испытуемые, имеющие низкие ранги по одному из них, будут иметь низкие ранги и по другому, а испытуемые, имеющие высокие ранги по одному из признаков, будут иметь по другому признаку также высокие ранги.
2. Две индивидуальные иерархии признаков, выявленные у двух испытуемых по одному и тому же набору признаков (например, личностные профили по 16-факторному опроснику Р. Б. Кеттелла).
Здесь ранжируются индивидуальные значения, полученные каждым из 2-х испытуемым по определенному (одинаковому для них обоих) набору признаков. Первый ранг получит признак с самым низким значением; второй ранг — признак с более высоким значением и т.д. Все признаки должны быть измерены в одних и тех же единицах, иначе ранжирование невозможно. Если индивидуальные иерархии двух испытуемых связаны положительно, то признаки, имеющие низкие ранги у одного из них, будут иметь низкие ранги и у другого, и наоборот.
3. Две групповые иерархии признаков.
Здесь ранжируются среднегрупповые значения, полученные в 2-х группах испытуемых по определенному, одинаковому для двух групп, набору признаков. В дальнейшем линия рассуждений такая же, как и в предыдущих двух случаях.
4. Индивидуальная и групповая иерархии признаков (индивидуальный и групповой профили).
Здесь ранжируются отдельно индивидуальные значения испытуемого и среднегрупповые значения по тому же набору признаков, которые получены, как правило, при исключении этого отдельного испытуемого — он не участвует в среднегрупповом профиле, с которым будет сопоставляться его индивидуальный профиль. Ранговая корреляция позволит проверить, насколько согласованы индивидуальный и групповой профили.
Пример 15:
Интеркорреляции шкал м. МПА
Пример 16:
Корреляции шкал м. МПА и м. УНП
Примечание к примеру 13: при корреляционном анализе необходимо обращать внимание на математический смысл тестовых показателей применяемых методик. В данном примере, чем выше тестовый показатель по шкалам м. МПА, тем выше мотивация к потреблению алкоголя. То же самое относится и к шкале "L" ("Ложь") м. УНП. Но шкалы "N" ("Невротизация") и "P" ("Психопатизация") м. УНП имеют противоположный смысл — чем выше арифметический тестовый показатель, тем ниже невротизация и психопатизация. Таким образом, отрицательная корреляция между тестовыми показателями м. МПА и шкалами "N" и "P" м. УНП в смысле их психологического содержания является положительной, т.е., чем выше выше мотивация, тем более выражена невротизация или психопатизация. Данный пример является наиболее типичным случаем возможной ошибки интерпретации результатов статистического анализа психологических исследований студентами психологических факультетов.
Заключение. Несмотря на то, что все приведенные выше статистические таблицы и графики были получены "нажатием одной клавиши", знания основ математической статистики еще никто не отменял. И эта программа также как и программа диагностики не более, чем виртуальное продолжение профессионализма её пользователей.